[LG]《Text Has Curvature》K Grover, H Zeng, Y Xia, C Faloutsos, G J. Gordon [CMU & Meta] (2026)
文本是否自带几何属性?本文给出了一个令人振奋的答案:文本不仅有曲率,而且这种曲率是语言天生的指纹,而非模型强加的产物。
这篇论文打破了以往将“曲率”视为模型架构选择的传统认知,将其定义为文本在双向推理中的内在特质。
以下是关于这项研究的深度拆解与启发性思考:
1. 语言不是平铺直叙的直线,而是充满起伏的几何
长期以来,我们习惯于将语言视为一串离散的符号,或者将其嵌入到欧几里得空间中。虽然有些研究尝试使用双曲几何来捕捉层级结构,但那更多是“给模型换个底座”。
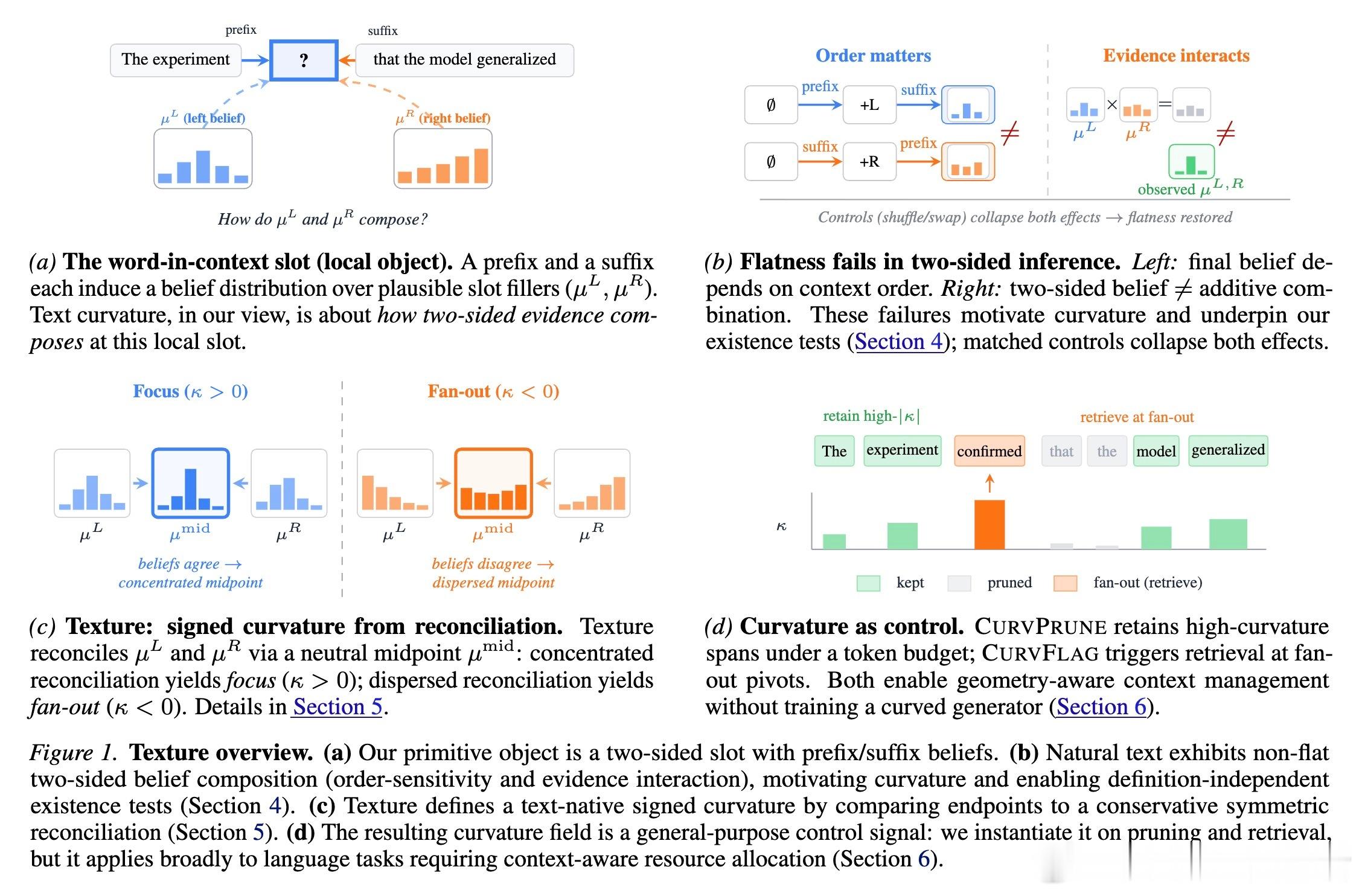
这项研究提出了一个本质的范式转移:曲率是文本在“双向推理”中表现出的属性。当你试图根据前文和后文来推测中间的一个词时,证据是如何融合的?这种融合过程中的非线性交互,就是文本自带的曲率。
金句:语言的意义并非均匀分布,它在逻辑的褶皱中弯曲,在共识的节点上聚焦。
2. 两个证明文本“非平坦”的实验证据
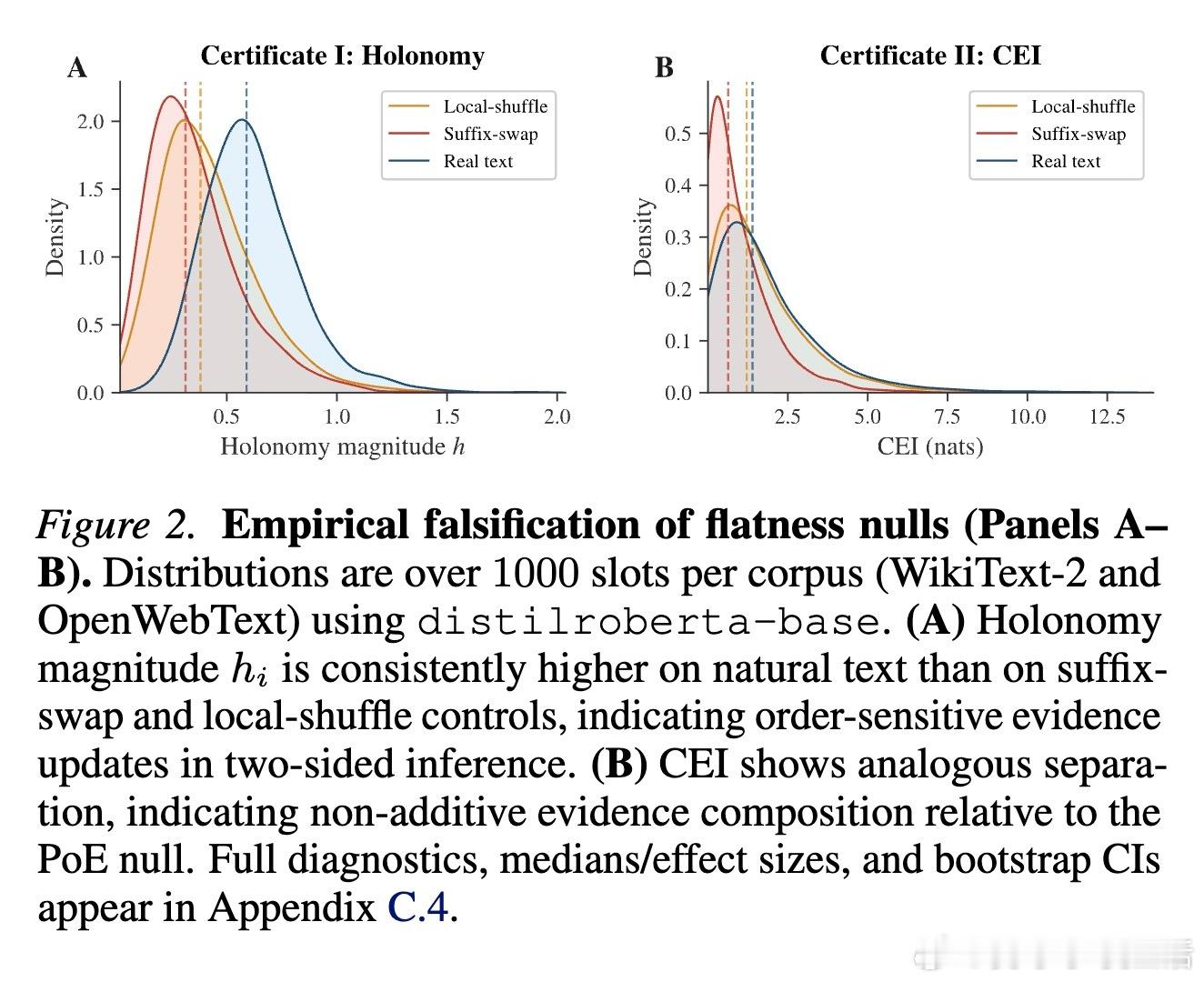
为了证明文本确实存在曲率,研究者设计了两个不依赖于任何特定定义的“平坦性虚无假设”:
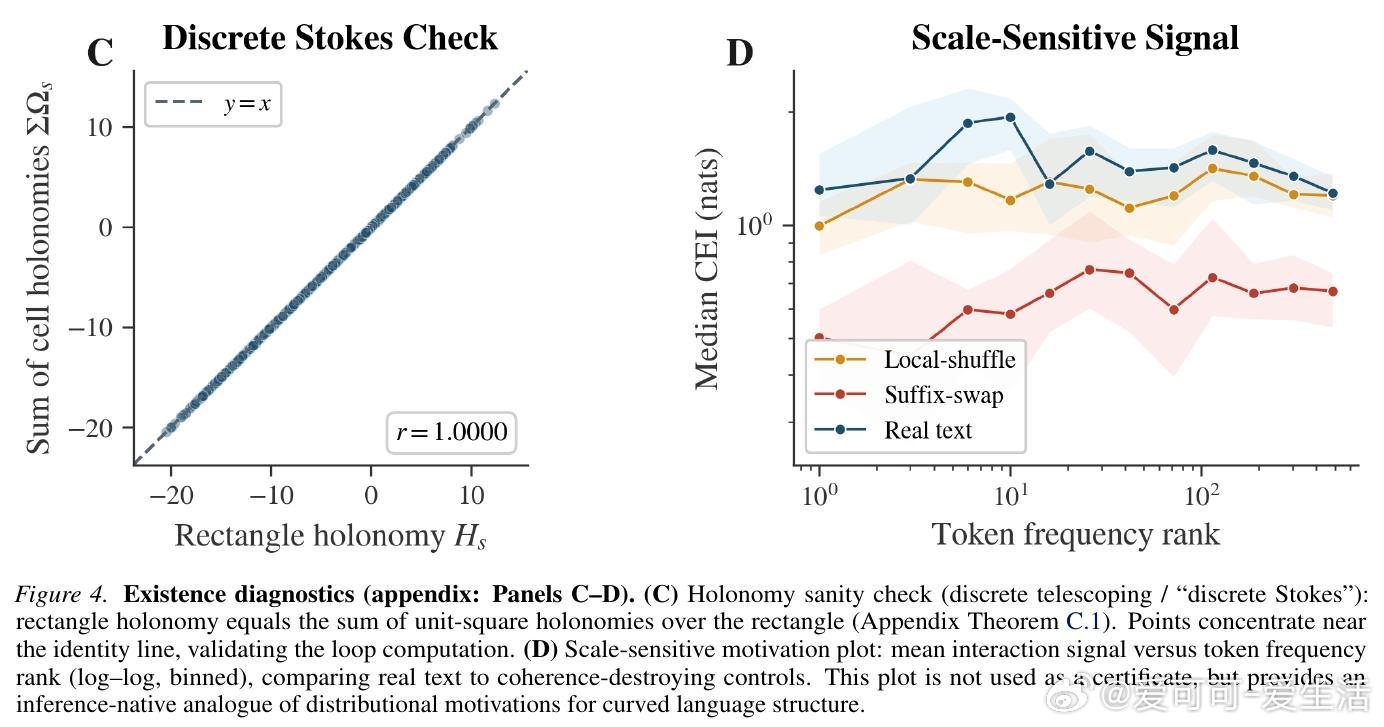
- 完整性验证(Holonomy):在平坦空间中,证据更新的顺序不应影响结果。但在自然语言中,先看左边再看右边,与先看右边再看左边的逻辑感知是完全不同的。- 证据加性验证(CEI):如果文本是平坦的,左右上下文对语义的贡献应该是简单的对数加法(Product-of-Experts)。实验发现,自然文本严重违反了这种加性,而随机打乱的文本则会回归平坦。
这证明了:文本的非平坦性是真实存在的,它是语义连贯性的必然结果。
3. 定义 Texture:语义的聚焦与发散
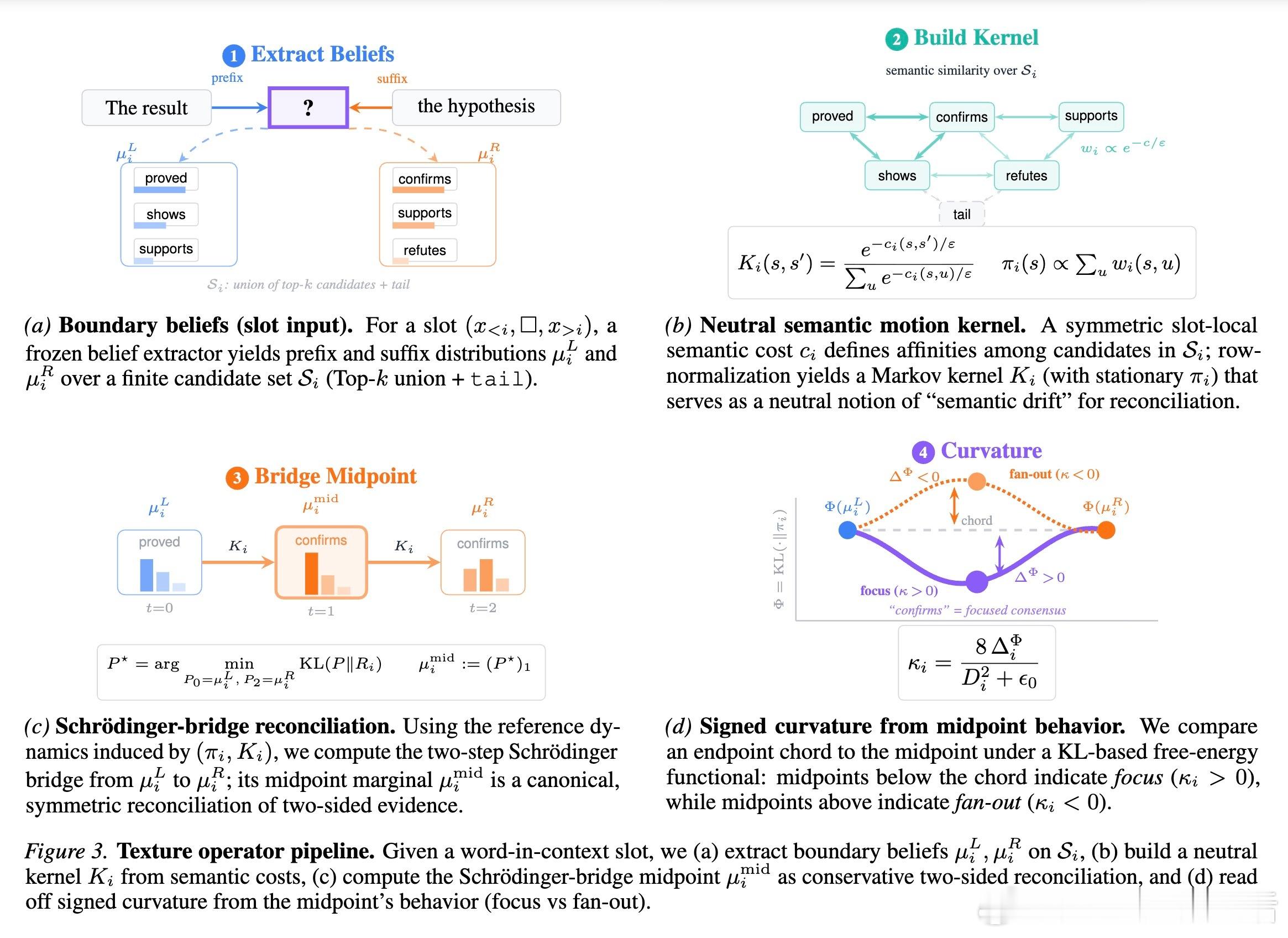
研究者引入了 Texture 这一概念来量化这种曲率。通过“薛定谔桥”(Schrödinger Bridge)算法,他们寻找左右信念在中间相遇时的最平滑路径:
- 正曲率(Focus):当左右上下文高度指向同一个明确的含义时,语义发生“坍缩”和聚焦。- 负曲率(Fan-out):当上下文诱导出多种竞争性的可能,或者语义指向不确定性时,语义发生“发散”。
金句:当上下文达成共识,意义便会坍缩聚焦;当预测指向未知,语义则如扇面般展开。
4. CurvPrune:循着几何的褶皱进行上下文压缩
既然文本有曲率,我们就可以利用它来管理长文本。CurvPrune 是一种基于曲率的提示词压缩技术。
它不再盲目地根据词频或重要性裁剪,而是优先保留那些曲率绝对值高的片段。这些片段要么是语义的“定海神针”(高正曲率),要么是逻辑的“关键分叉点”(高负曲率)。实验证明,这种方法在长文档问答中比传统的压缩方法更有效。
微故事:面对冗长的信息洪流,我们不再粗暴地截断,而是像地质学家寻找矿脉一样,保留那些承载了语义重量的“几何高地”。
5. CurvFlag:在语义迷雾最浓处触发检索
在检索增强生成(RAG)中,什么时候该查资料?CurvFlag 给出了几何解释:当文本表现出明显的“负曲率”(发散)时,说明局部上下文已经不足以支撑确定的推理。
此时,曲率信号就像一个自动触发器,告诉模型:这里的语义正在流失,请立即调用外部知识。这种方法无需额外训练,就能显著提升模型在多跳推理任务中的效率。
金句:曲率是智能体的指南针,它在语义迷雾最浓处提示我们:是时候向外寻求答案了。
6. 几何不再是底座,而是文本自带的灵魂
这项研究最深刻的启示在于,我们或许不需要费力去训练“双曲模型”或复杂的几何架构。如果文本本身就带有曲率,我们只需要学会如何“测量”它。
通过测量曲率,我们获得了一个通用的、无需训练的控制原语。它不仅能优化计算资源,还能让我们更深入地理解 LLM 到底在处理什么样的空间。
最高级的智能,或许不在于创造复杂的结构,而在于洞察并顺应事物本身的几何。
arxiv.org/abs/2602.13418