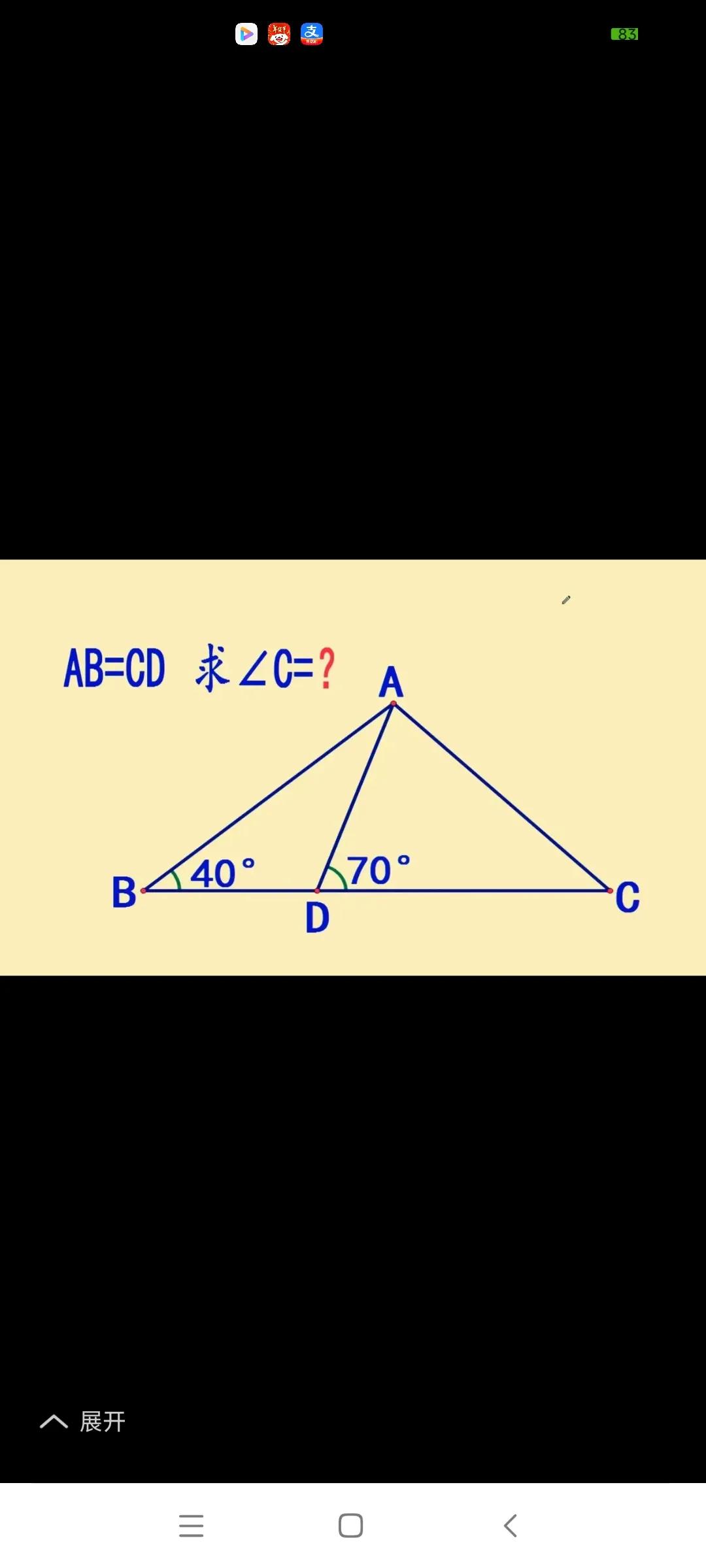
实际学习的过程就是提高自己完善自己的过程。曾经一直有人鼓吹读书无用论。不是无用,而是我们不用。也许在不知不觉中,看似枯燥的知识在潜移默化的改变我们的生活,提高着我们的工作效率和生活质量。 学习的过程就是提出问题解决问题的过程。我们无时无刻的不在解决生活和工作中的问题,无时无刻不在学习充实完善提高自我,提出问题解决问题的过程也是充实完善提高自我的过程。 比如下面这道题。它是一个三角形,我们要求证一个角的度数,就要寻找求证这个问题的条件。什么条件呢?知道了两个角的度数,知道了一个边和另一个边的关系。这就需要根据所学进行推理和求证,这就需要建立一个已知和未知的桥梁。建立已知和未知的桥梁有什么方法呢?有桥梁我们可以直接走过去,1+1等于2,简单明了,张口就来。张口就来的问题就不叫问题了。有的没有桥梁,有的有桥梁还是过不去。这就需要我们有材料,并且运用这些材料去搭一座由已知通向未知的桥梁从而通过它到达未知的彼岸。 这道题的材料有哪些呢?要求证什么问题呢?它知道了这个三角形的一个角的度数,然后搭了一座桥,在最长的边上以一个边为长度取了个点,并且和对角连起来。这个连线就成了一座通向未知的桥。 可我们发现,即使通过已知的材料,通过各种所学的知识,并不能直接到达未知的彼岸。那我们就还得建一座桥,一座能够到达未知彼岸的桥,建立起和这个要求证的角的联系。以初中所学的知识。很显然是通过全等三角形来搭桥的,通过等边三角形建立起一座从一个角到另一个角的桥梁,从一个三角形到另一个三角形的桥梁,从而从已知的此岸到达未知的彼岸。 既然可以从三角形的一个边可以划出一个独立的一部分,我们可以用同样的方法从另一边划出一个同样独立的部分,并且是放在了有同一个顶点的三角形里。那么桥就来了。既然这个三角形的两边相等,知道一个角,其他的角就迎刃而解了。这里又用到了外角和内角的关系,三个角的关系,所以熟悉并运用知识点很重要。学习的过程就是运用这些知识点求证的过程,也是一个搭桥的过程。很显然通过角的度数知道了边的关系,建立了两个已知和未知的小三角形的桥梁,从而也建立了从已知到未知的两个角的桥梁。 我们的生活和工作中也是通过建立各种桥梁,通过不断的发现问题,提出问题,解决问题到达人生的彼岸,从而走向高远,破浪前行。所以我们要明白知识的重要,方式方法的重要,桥梁的重要,集思广益的重要,开拓进取的重要。 少壮不努力,老大徒伤悲。我一直到中学数学一直很好,用老师的话来说叫通门,很多难题都能拨开乌云见青天。可后来呢?不学了,你不学怎么会解决问题啊?感觉没有人家精通高等数学的思路宽,能力强。甚至有时候有种无路可走的感觉。 所以,生活和工作的高手也是学习的高手,也是提出问题发现问题解决问题的高手。而没有这种能力的人自然成了高质量生活的弃儿。否则连后悔的时间都没有。 这也是我的一个教训吧。[祈祷] 我们的人生就是一张张考卷。自问我们鞥做到哪一步,哪一题呢?做到附加题甚至满分的也许有吧。我感觉自己不及格,但希望余生能让自己及格,感觉还有这个时间和精力,也必须有这个时间和精力。 时不我待,百废待兴啊!