据说中国学者王虹解决了一个大问题，能得菲尔兹奖
问题叫Kakeya猜想，挂谷猜想，1917年提出。从年头就能看出是一个大问题。王虹北大数学院2007级，MIT博，目前是纽约大学库朗数学研究所副教授，2022年得了科学突破奖，已经是希望之星。
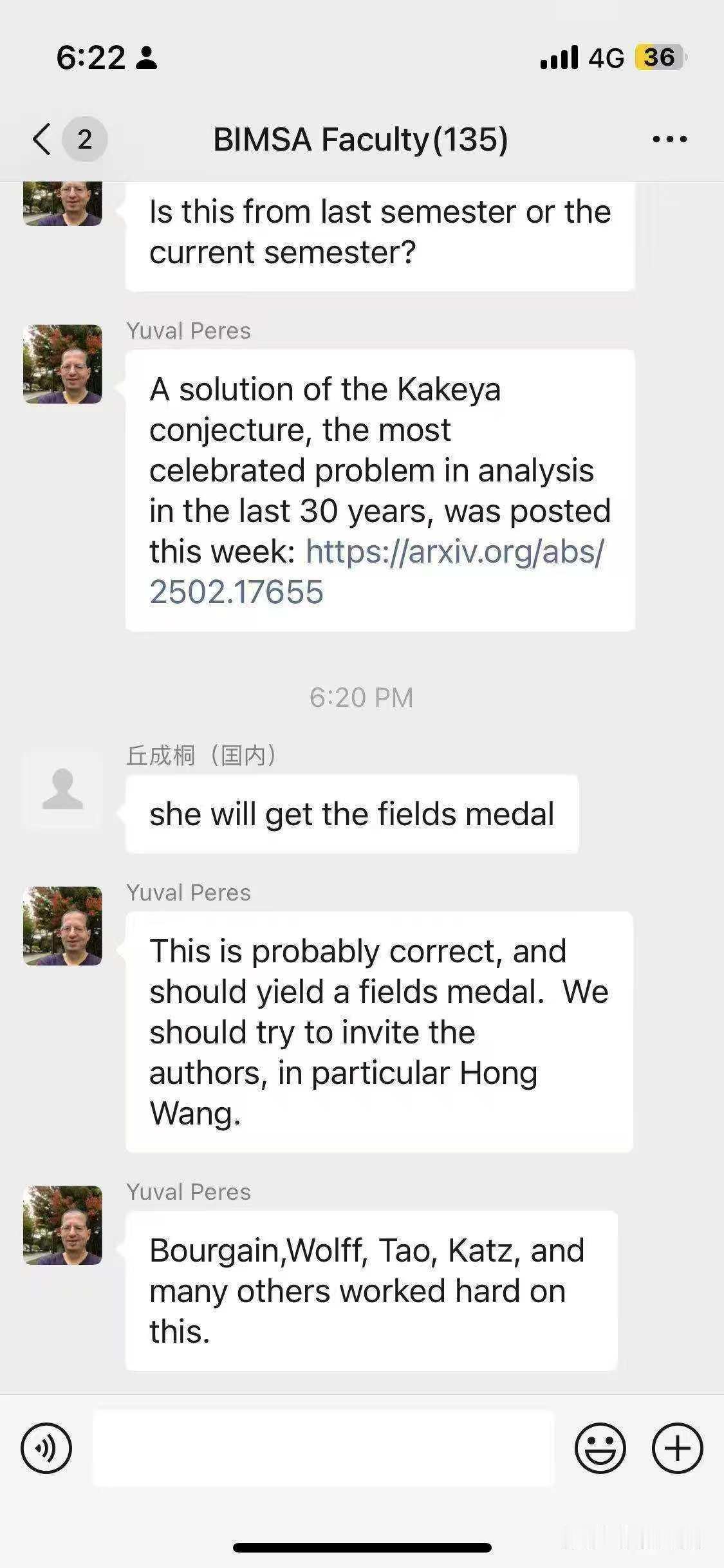
论文2月26日刚发出来，大家在读。图三大佬似乎比较认可。
这个问题是说，在欧几里得空间中，一个包含所有方向单位线段的集合（称为Kakeya集）的最小测度是多少。具体来说，猜想指出，在空间中，Kakeya集的测度不可能任意小。
测度这个名词不要怕。一维就是长度，二维就是面积，三维就是体积。这些空间里，包含所有方向的线段的东西，可以体积任意小。这结论有些反直觉。
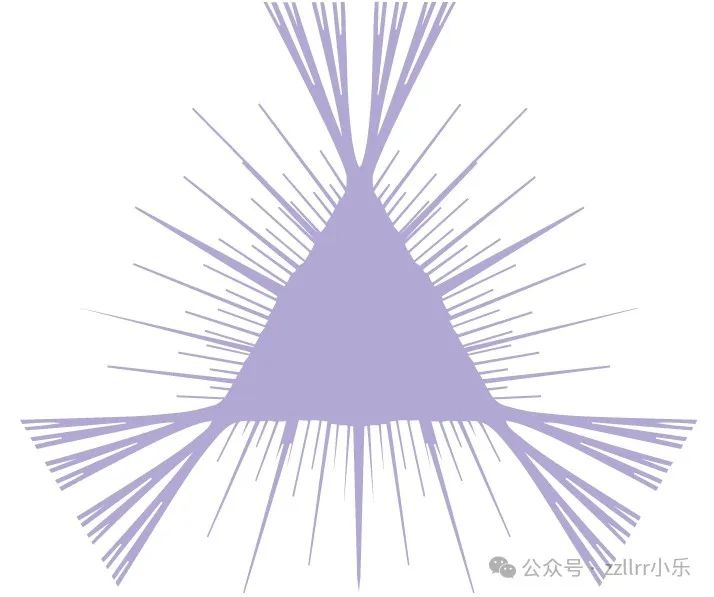
直觉解释，就是一根针（有长度但无限细）在空间中乱扫，扫过的最小面积是多少？最简单直觉是一个圆，面积不为0。但是如果针可以巧妙排列，那么面积就可以很小。但应该不是零。
如图四，这种排列覆盖所有方向，但是面积远小于圆。把它继续往极限里推，面积还能缩小，也许就到零了？
现在，王和合作者证明，不是零，在三维里不是。
