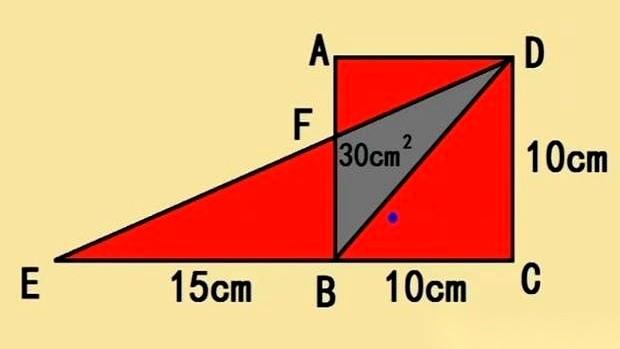
就这道小学几何题,据说第一眼看过去,不少大学生都把笔放下了。 一个边长10的正方形,旁边多出来一块三角形,面积告诉你了,是30。然后又给了一条斜边,BE长15。 让你求两个红色阴影区的总面积。 问题就出在这条斜边BE上。很多人盯着它,想用勾股定理,想算角度,脑子里辅助线画得天花乱坠,结果把自己绕进去了。 可你把图换个角度看,就一秒钟的事。 那个在正方形外面的三角形BDE,它的面积是怎么算的?底乘以高除以二,对吧? 它的底是DE,高呢?从B点垂直往下画一条线,这条高,不多不少,正好就是正方形的边长——10。 现在面积和高都有了。 面积30,高是10,那底DE的长度,不就是6吗? 算到这,图里最大的那块红色三角形ADE的面积,一下就出来了。底是AD(10)加上DE(6),高是CD(10),面积就是(10+6)×10÷2,等于80。 别急,还没完。 题目里给的那个小三角形BDE,面积是30。它和旁边那个没上色的空白三角形BDC,是同一个高(都是10),但底不一样。 空白三角形BDC的底是10,高是10,面积就是50。 现在,用那个最大的红色三角形ADE的面积80,减去空白三角形BDC的面积50,剩下的是什么? 就是那两个红色阴影区的面积之和:30。 所以说,有时候解题不是比谁算的快,是比谁看得穿。那个BE=15,从头到尾就是个烟雾弹。