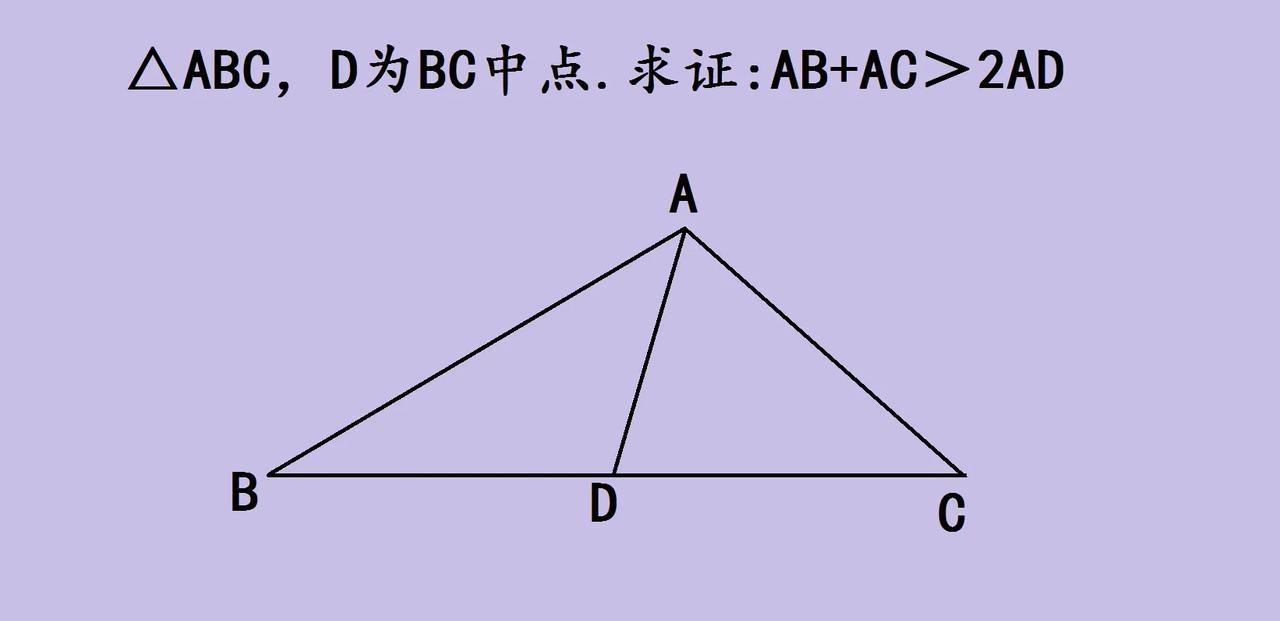
铁子们，来看这道初中几何题！△ABC 中，D 是 BC 中点，要证 AB + AC ＞ 2AD 。 这题关键在“构造”！想到延长 AD 到 E，让 DE = AD ，再连 CE ，瞬间把分散的线段关联起来～ 构造后，△ABD 和△ECD 全等（SAS 判定 ），AB 就转化成 CE 。这时看△ACE ，根据三角形三边关系，AC + CE ＞ AE ，而 AE 是 2AD ，AB 又等于 CE ，所以 AB + AC ＞ 2AD 就证出来啦！ 这种构造辅助线的思路，把看似无关的线段“搬”到一个三角形里，利用全等和三边关系解题，超经典～ 初中几何常考这类转化思想，掌握了构造法，难题也能变简单！ 有没有被这种巧妙思路惊艳到？快给孩子讲讲，培养几何思维超有用。
评论列表
猜你喜欢
【1评论】【6点赞】
【3评论】【14点赞】
【1点赞】
【5评论】【3点赞】
【2评论】【1点赞】
【2评论】【8点赞】
【1评论】【35点赞】
作者最新文章
热门分类
体育TOP
体育最新文章
用户10xxx32
说实话，这题我解了，但是作为一个孩子，这种发散性思维需要偶然性，有点难，一个孩子喜欢这种发散性思维，会很简单，但是其他的方面会精力不足（天才少年少女除外），孩子除了学习以外还有成长