[LG]《Quantitative Bounds for Length Generalization in Transformers》Z Izzo, E Nichani, J D. Lee [NEC Labs America & Princeton University & UC Berkeley] (2025)
在深度学习领域,Transformer模型的“长度泛化”(Length Generalization, LG)能力,即模型在训练时只见过较短序列,却能在测试时处理远长于训练序列的输入,至关重要但尚不完全明晰。本文首次给出了Transformer实现长度泛化所需的训练序列长度的定量界限,系统性地解析了不同模型复杂度和计算精度下的LG表现。
核心观点与贡献如下:
1. 问题背景与动机
- 先前研究仅证明Transformer在训练序列长度超过某阈值后能实现LG,但未明确该阈值大小。
- 本文基于Huang等人提出的“极限Transformer”理论,探讨何时短序列训练足以模拟长序列行为,从而实现泛化。
2. 理论框架与分析
- 区分有限精度(finite precision)与无限精度(infinite precision)下的注意力机制,分别对应实际硬件限制与理论理想情况。
- 分析一层和两层Transformer,分别给出对应的最小训练长度界限。
- 引入“硬注意力(hardmax)”行为,阐明当训练序列足够长时,有限精度softmax注意力趋近于硬注意力,简化分析。
- 证明LG发生的关键是长序列上的模型内在行为能被训练中见过的短序列“模拟(simulate)”,这为训练长度需求提供了直观且统一的解释。
3. 主要定理精要
- 定理4.1(有限精度单层Transformer,worst-case误差控制):训练长度N呈多项式关系增长,依赖于模型参数范数、位置编码周期性(вҲҶ)、局部性参数(П„)、词汇表大小(|ОЈ|)及误差倒数(Оө⁻¹)。
- 定理4.2(有限精度单层Transformer,平均误差控制):在词汇分布满足Dirichlet先验假设下,LG同样成立,且训练长度界限可显式计算。
- 定理5.2(无限精度两层Transformer):训练长度界限依赖复杂度度量C(f),该度量指数增长于模型权重范数,体现深层模型表达力与训练需求的权衡。
4. 实验验证
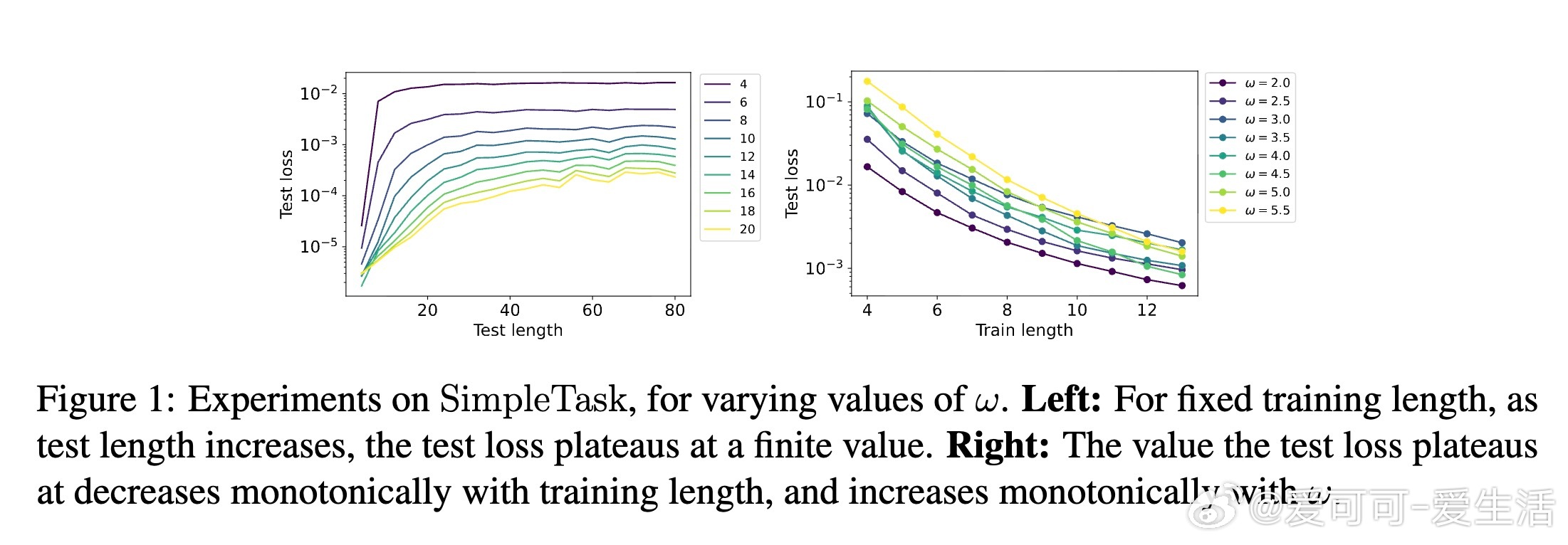
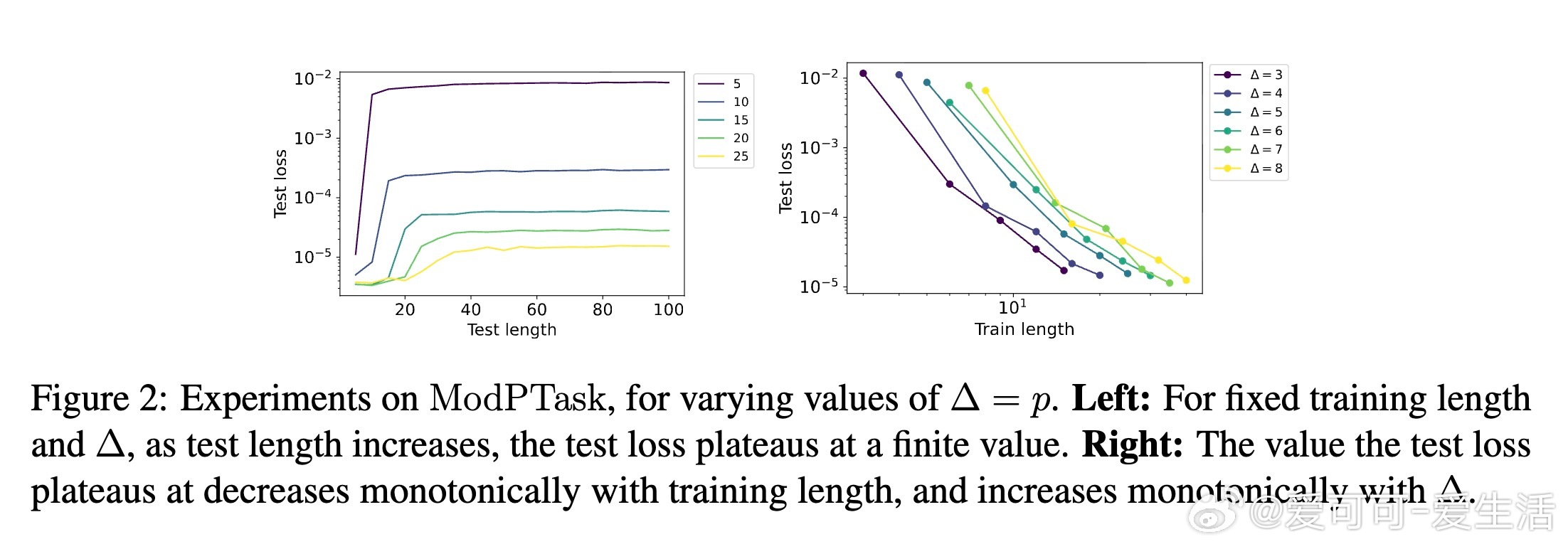
- 设计SimpleTask和ModPTask两种合成任务,实证验证训练长度对LG的影响,与理论界限保持一致。
- 观察到随着训练长度增加,模型在更长测试序列上的误差趋于稳定且下降,支持训练长度对泛化能力的决定性作用。
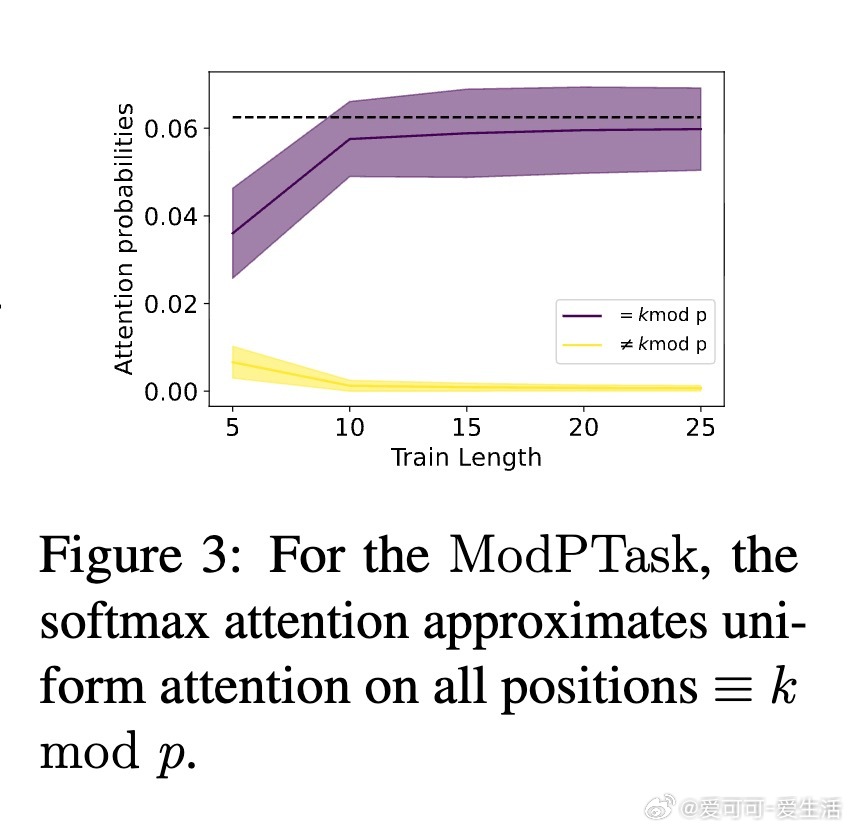
- 通过注意力热力图验证有限精度下的硬注意力假设合理性。
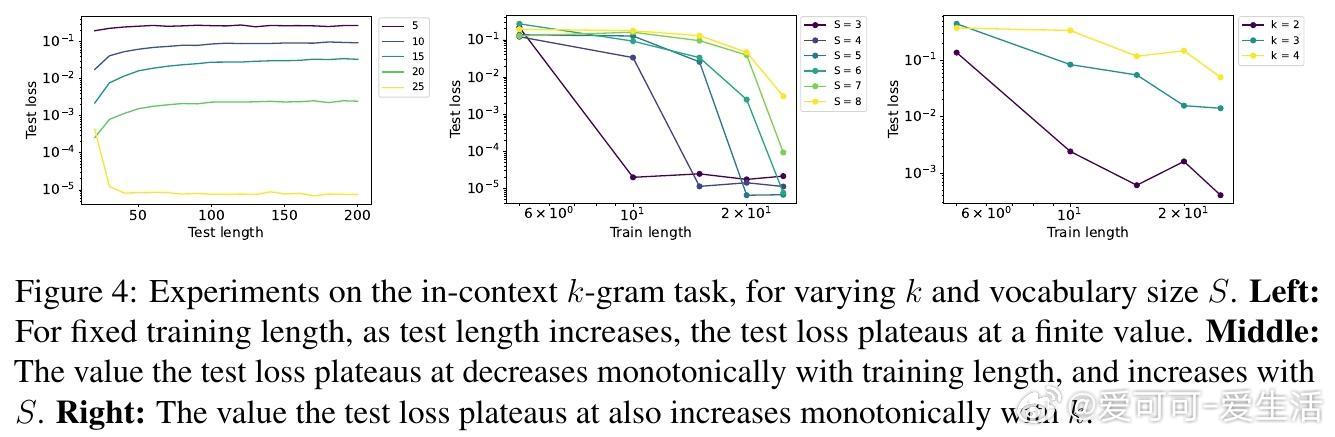
- 两层Transformer在in-context k-gram任务上的测试结果进一步印证了复杂度度量对训练长度的影响。
5. 理论与实践意义
- 解析了Transformer泛化到更长序列所需训练长度的定量规模,明确了参数规模、位置编码周期、词汇大小等因素的作用。
- 通过“模拟短序列”的思想,构建了理解和设计更佳长度泛化Transformer的理论基石。
- 为未来设计更深层、更高效且具备强泛化能力的Transformer模型提供理论指导。
6. 未来方向
- 扩展至更深层Transformer结构,关联训练长度与C-RASP程序复杂度。
- 拓展平均误差分析至更广泛的序列分布。
- 探索不同位置编码方案对训练长度及LG能力的影响。
总结而言,本文突破了此前长度泛化理论的模糊界限,首次给出了Transformer实现稳健长度泛化的明确训练序列长度下界,结合有限与无限精度分析,理论与实证相辅相成,深化了对Transformer泛化机制的理解。
全文详见:arxiv.org/abs/2510.27015